linermountain.blogg.se - Average of 2 percentages calculator

AVERAGE OF 2 PERCENTAGES CALCULATOR HOW TO
AVERAGE OF 2 PERCENTAGES CALCULATOR FREE

The percent value is computed by multiplying the numeric value of the ratio by 100.

AVERAGE OF 2 PERCENTAGES CALCULATOR FREE

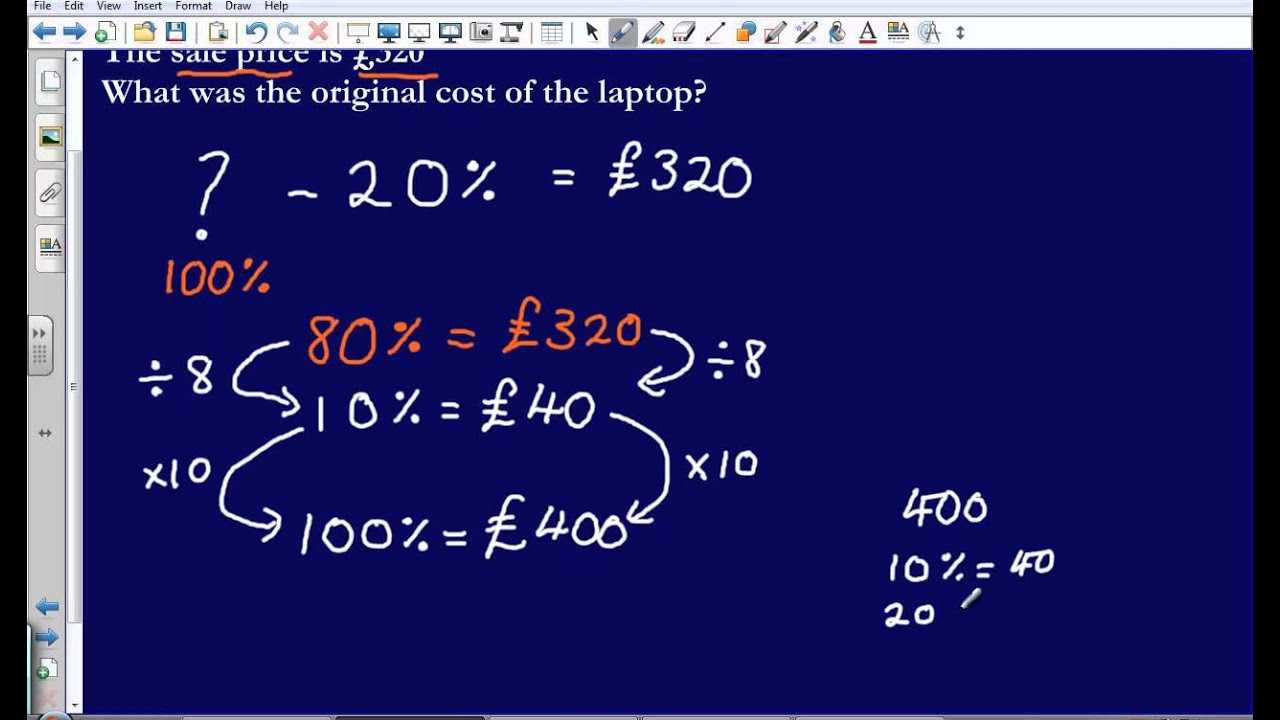
Synopsis: Free online instant calculator for finding a percentage of a number as well as reverse percentage calculations. On This Page: Summary - Defining Percentage - Main Article - About/Author $\alpha = $ (the number of misses) and $\beta = $ (total number of transactions $-$ the number of misses).Peer-Reviewed: N/A - Publication Type: Conversion / Calculation The parameters of the beta distribution would be e.g. If that probability is below some pre-defined level (for example the above mentioned 0.05), you'd consider it an anomaly.įor completeness: If you want to be even more precise (which I doubt, considering that you were given a wrong task in the first place), you can get a confidence interval of $p$ by modelling it by the beta distribution, and use the extreme, but still plausible $p$ in the above binomial distribution. Having all this, you can calculate the cumulative probability of observing at least as many misses as you actually had in the month in question. You can estimate $p$ from historical data, as the fraction of the total number of misses and the total number of transactions in the past months. With $n$ being the number of transactions and $k$ the number of misses in the month in question. Without having further domain knowledge of your data, the best you can do is to use the binomial distribution: You need to use a different, more appropriate probability distribution. However, your percentages are not normally distributed! As Richard Hardy pointed out in his comment, two SDs above the mean are already impossible to achieve, as it would be above 100%. That's presumably the reason why you were asked to compute these values.

If your percentages were normally distributed, you could easily derive it from the mean and the standard deviation: values that are more than 2 SDs away from the mean appear with probability below 0.05.

AVERAGE OF 2 PERCENTAGES CALCULATOR HOW TO

So the question remains how to calculate this probability.

If it is very improbable (say, probability below 0.05), you may consider it to be anomalous. The best you can do is to calculate the probability:Īssuming a known probability of a transaction to be a "mis", how probable is to have the given number of misses in a month? There is no clear-cut answer to that question. Is the number of missed transactions within what could be considered "normal", or does it deviate so much to be considered anomalous? For you use, at least as I understand it, it seems to be incorrect.Īs I understand from your question and comment, you are trying to do anomaly detection.

Alternatives determining spread and central tendency for percentages over a period of time.įor example, would the following be incorrect to do assuming that the percentages represent # transactions missed / # total transactions for each different months with the same calculation being used for each month: Month Dataįrom this post is seems like it should be done with weighted averages since the totals are different, and that calculating the mean and standard deviation is possible for percentages only if they come from the same total, meaning the above would be incorrect and that I would need additional information to determine the weight to multiple the percentages by, if that is correct.Īs others have pointed out, whether it is correct to calculate the mean and the standard deviation of percentages depends on your intended use.

What conditions are needed in order to calculate the mean and standard deviation for percentages,.

If the mean and standard deviation for percentages can be calculated,.

some other method (weighted averaged) since I do not have any other information other than the percentages. I was asked to calculate the mean and standard deviation, but I am unsure if the result would be meaningful and if the mean could be calculated for percentages in the traditional sense (e.g., in Excel doing AVERAGE(percent array)) vs. The percentages are for 13 months and ranging from 97 to 99 percent. My data is some percentages on how many transactions from a whole are missed each month.